Bài 1 (trang 59 SGK Hình học 10): Cho tam giác ABC vuông tại A, B̂ = 58o và cạnh a = 72cm. Tính Ĉ, cạnh b và đường cao ha.
Lời giải:
+ Ĉ + B̂ = 90º ⇒ Ĉ = 90º - B̂ = 90º – 58º = 32º
+ b = a.sinB = 72 . sin 58º ≈ 61,06 cm
+ c = a . cos B = 72 . cos 58º ≈ 38,15cm
+ ha = c . sin B = 38,15 . sin 58º = 32,36 cm.
Bài 2 (trang 59 SGK Hình học 10): Cho tam giác ABC biết các cạnh a = 52,1cm, b = 85cm, c = 54cm. Tính các góc Â, B̂, Ĉ.
Lời giải:
Kiến thức áp dụng
Tam giác ABC có AB = c, BC = a, CA = b thì:
Bài 3 (trang 59 SGK Hình học 10): Cho tam giác ABC có Â = 120o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.
Lời giải:
+ a2 = b2 + c2 - 2.bc.cosA = 82 + 52 – 2.5.8.cos120º = 129
⇒ a = √129 cm
Kiến thức áp dụng
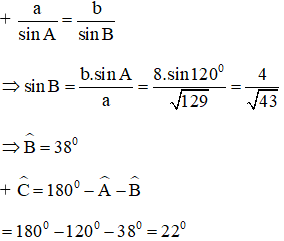
Trong tam giác ABC có AB = c, BC = a, CA = b có:
+ a2 = b2 + c2 – 2.bc.cos A
Bài 4 (trang 59 SGK Hình học 10): Tính diện tích S của tam giác có số đo các cạnh lần lượt là 7, 9 và 12.
Lời giải:
Nửa chu vi của tam giác: p = (7 + 9 + 12)/2 = 14.
Áp dụng công thức Hê–rông ta có:
Kiến thức áp dụng
Công thức Hê–rông tính diện tích:
Tam giác có ba cạnh lần lượt là a, b, c, nửa chu vi p = (a + b + c) / 2 thì diện tích bằng:
Bài 5 (trang 59 SGK Hình học 10): Cho tam giác ABC có Â = 120o. Tính cạnh BC, cho biết cạnh AC = m và cạnh AB = n.
Lời giải:
Áp dụng định lý côsin ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos A
= m2 + n2 – 2.m.n.cos120º
= m2 + n2 + mn.
⇒ BC = √( m2 + n2 + mn).
Kiến thức áp dụng
Định lý côsin: Tam giác ABC có:
AB2 = AC2 + BC2 – 2.AC.BC.cosC
AC2 = BC2 + BA2 – 2.BC.BA.cosB
BC2 = AB2 + AC2 – 2.AB.AC.cosA.
Bài 6 (trang 59 SGK Hình học 10): Tam giác ABC có các cạnh a = 8cm, b = 10cm và c = 13cm.
a) Tam giác đó có góc tù không?
b) Tính độ dài trung tuyến MA của tam giác ABC đó.
Lời giải:
a) Ta có:
Vậy tam giác ABC có góc C tù.
b) Ta có:
Kiến thức áp dụng
+ Định lý Côsin: Trong tam giác ABC có AB = c, BC = a, CA = b ta có:
+ Công thức tính độ dài đường trung tuyến: 
Bài 6 (trang 59 SGK Hình học 10): Tam giác ABC có các cạnh a = 8cm, b = 10cm và c = 13cm.
a) Tam giác đó có góc tù không?
b) Tính độ dài trung tuyến MA của tam giác ABC đó.
Lời giải:
a) Ta có:
Vậy tam giác ABC có góc C tù.
b) Ta có:
Kiến thức áp dụng
+ Định lý Côsin: Trong tam giác ABC có AB = c, BC = a, CA = b ta có:
+ Công thức tính độ dài đường trung tuyến:
Bài 8 (trang 59 SGK Hình học 10): Cho tam giác ABC biết cạnh a = 137,5cm, ∠B = 83o và ∠C = 57o. Tính góc A, bán kính R của đường tròn ngoại tiếp, cạnh b và c của tam giác.
Lời giải:
Kiến thức áp dụng
Định lý sin : Trong tam giác ABC có AB = c, BC = a, CA = b, bán kính đường tròn ngoại tiếp R ta có :
Bài 9 (trang 59 SGK Hình học 10): Cho hình bình hành ABCD có AB = a, BC = b, BD = m, AC = n. Chứng minh rằng: m2 + n2 = 2(a2 + b2).
Lời giải:
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).
Kiến thức áp dụng
Tam giác ABC có trung tuyến AM thì :
Bài 10 (trang 60 SGK Hình học 10): Hai chiếc tàu thủy P và Q cách nhau 300m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển người ra nhìn chiều cao AB của tháp dưới các góc ∠BPA = 35o và ∠BQA = 48o. Tính chiều cao của tháp.
Lời giải:
Kiến thức áp dụng
* Lưu ý: Trong các bài toán này ta cần đến sự trợ giúp của máy tính CASIO, tuy nhiên ta chỉ có thể tính các giá trị lượng giác sin, cos, tan.
Ta đã biết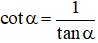 
nên để tính cot α ta đi tính 1/tan α.
Ví dụ : Để tính cot 35º ta ấn :
(Kết quả cot 35º = 1,428).
#soanbaitap
Không có nhận xét nào:
Đăng nhận xét