Bài 1 (trang 49 SGK Hình học 12): Tìm tập hợp tất cả các điểm M trong không gian luôn luôn nhìn một đoạn thẳng AB cố định dưới một góc vuông.
Lời giải:
+ Gọi O là trung điểm của AB.
Tam giác AMB là vuông tại M có OM là đường trung tuyến ứng với cạnh huyền nên : 
Suy ra, M thuộc mặt cầu tâm O, bán kính là 
+ Ngược lại, xét mặt cầu 
với O là trung điểm của AB.
Lấy điểm M bất kì thuộc mặt cầu này. Suy ra: 
(2)
Từ (1) và (2) suy ra:
⇒ Tam giác MAB vuông tại M.
Kết luận: Vậy tập hợp các điểm M trong không gian luôn nhìn đoạn thẳng AB cố định dưới 1 góc vuông là mặt cầu 
Bài 2 (trang 49 SGK Hình học 12): Cho hình chóp tứ giác đều S.ABCD có cạnh đều bằng a. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp đó.
Lời giải:
S.ABCD là hình chóp tứ giác đều cạnh đều bằng a
⇒ ABCD là hình vuông cạnh a và SA = SB = SC = SD = a.
Gọi O là hình chiếu của S trên (ABCD).
⇒ O là tâm hình vuông ABCD
⇒ OA = OB = OC = OD = OS.
⇒ O là tâm mặt cầu ngoại tiếp hình chóp S.ABCD,
bán kính mặt cầu là 
Bài 3 (trang 49 SGK Hình học 12): Tìm tập hợp tâm các mặt cầu luôn chứa một đường tròn cố định cho trước.
Lời giải:
Gọi I là tâm của mặt cầu chứa đường tròn (C) cố định cho trước.
⇒ I cách đều tất cả các điểm M thuộc đường tròn (C)
⇒ I nằm trên đường thẳng đi qua tâm của đường tròn (C) và vuông góc với mặt phẳng chứa (C).
Bài 4 (trang 49 SGK Hình học 12): Tìm tập hợp tâm các mặt cầu luôn cùng tiếp xúc với ba cạnh của một tam giác cho trước.
Lời giải:
* Xét mặt cầu (S) tâm J, bán kính R và tiếp xúc với ba cạnh: AB, BC, AC lần lượt tại M, N và P.
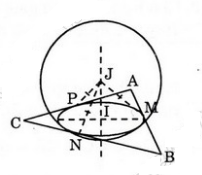
Gọi I là hình chiếu vuông góc của J lên mp (ABC) ⇒ IJ ⊥ (ABC)
* Ta có: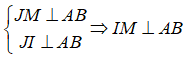 
(định lí 3 đường vuông góc)
Chứng minh tương tự có: 
(1)
* Xét ba tam giác JIM; JIN và JIP có:
⇒ ∆ JIM = ∆ JIN = ∆JIP (ch- cgv)
⇒ IN = IM = IP (2)
Từ (1) và (2) suy ra, I là tâm đường tròn nội tiếp tam giác ABC.
* Lấy điểm J thuộc trục đường tròn nội tiếp tam giác ABC.
Đường tròn nội tiếp tam giác ABC tiếp xúc với ba cạnh AB, BC và CA lần lượt taị M, N và P.
Ta có: 
(1)
Mặt khác; IM = IN = IP = r.
⇒ ∆ JIM = ∆ JIN = ∆JIP (c-g-c)
⇒ JM = JN = JP (2)
Từ (1) và (2) suy ra, mặt cầu (S) tâm J tiếp xúc với ba cạnh của tam giác ABC.
Vậy tập hợp tâm các mặt cầu tiếp xúc với ba cạnh của tam giác ABC cho trước là trục đường tròn nội tiếp tam giác ABC,
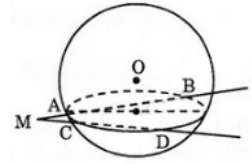
Bài 5 (trang 49 SGK Hình học 12): Từ một điểm M nằm ngoài mặt cầu (O; R), vẽ hai đường thẳng cắt mặt cầu lần lượt tại A, B và C, D.
a) Chứng minh rằng MA.MB = MC.MD
b) Gọi MO = d. Tính MA.MB theo R và d.
Lời giải:
a) Hai đường thẳng MAB và MCD giao nhau xác định một mặt phẳng (P). Mặt phẳng (P) cắt mặt cầu theo giao tuyến là đường tròn (C), ngoại tiếp tứ giác phẳng ABCD.
Xét ΔMAC và ΔMDB có:
⇒ MA.MB = MC.MD (đpcm).
b) Giả sử đường thẳng MO cắt mặt cầu tại P và Q.
Theo kết quả phần a) ta cùng có:
MA.MB = MP.MQ
Mà MP.MQ = (MO – OP)(MO + OQ) = (d – r)(d + r) = d2 – r2.
Vậy MA.MB = d2 – r2.
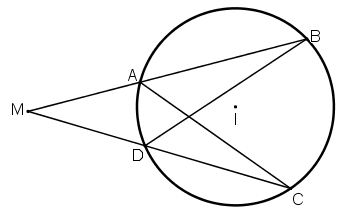
Bài 6 (trang 49 SGK Hình học 12): Cho mặt cầu (O; R) tiếp xúc với mặt phẳng (P) tại I. Gọi M là một điểm nằm trên mặt cầu nhưng không phải là điểm đối xứng với I qua tâm O. Từ M ta kẻ hai tiếp tuyến của mặt cầu cắt (P) tại A và B. Chứng minh rằng góc (AMB)= góc (AIB)
Lời giải:
* Do mặt cầu S(O; r) tiếp xúc với mp (P) tại I nên: OI ⊥ (P) ⇒ OI ⊥ IA
Suy ra, AI là tiếp tuyến của mặt cầu đã cho tại điểm I.
Ta có AM và AI là hai tiếp tuyến cắt nhau tại A của mặt cầu nên:
AM = AI ( tính chất hai tiếp tuyến cắt nhau)
* Tương tự có BM = BI.
* Xét hai tam giác AMB và tam giác AIB có:
AM = AI
BM = BI
AB chung
Suy ra: ∆ AMB = ∆ AIB ( c.c.c)
Bài 7 (trang 49 SGK Hình học 12): Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, AD = c.
a) Hãy xác định tâm và bán kính của mặt cầu đi qua 8 đỉnh của hình hộp đó.
b) Tính bán kính của đường tròn là giao tuyến của mp(ABCD) với mặt cầu trên.
Lời giải:
Soanbaitap.com gửi đến các bạn học sinh đầy đủ những bài giải toán 12 có trong sách giáo khoa tập 1 và tập 2, đầy đủ cả phần hình học và đại số. Tổng hợp các công thức, giải bài tập toán và cách giải toán lớp 12 khác nhau.
#soanbaitap
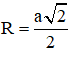
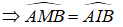
Không có nhận xét nào:
Đăng nhận xét