Bài 1 (trang 155 SGK Đại số 10): Hãy nêu định nghĩa của sinα , cosα và giải thích vì sao ta có :
sin(α +k2 π)=sinα;k ∈Z
cos(α +k2 π)=cosα;k ∈Z
Lời giải
+) Định nghĩa của sin α; cos α
Trên đường tròn lượng giác, xét cung AM có số đo α
Gọi H và K lần lượt là hình chiếu của M trên trục Ox, Oy.
Tung độ y = OK¯ của điểm M được gọi là sin của α : sin α = OK¯
Hoành độ x = OH¯ của điểm M được gọi là cos của α : cos α = OH¯
Trên đường tròn lượng giác trong mặt phẳng Oxy, lấy điểm A (1; 0) làm gốc.
Khi đó các cung có số đo hơn kém nhau một bội của 2π có điểm cuối trùng nhau.
Giả sử cung α có điểm cuối là M(x; y)
Khi đó với mọi k ∈ Z thì cung α + k2π cũng có điểm cuối là M.

sin α = y, sin (α + k2π) = y nên sin(α + k2π) = sinα
cos α = x, cos(α + k2π) = x nên cos(α + k2π) = cosα
Bài 2 (trang 155 SGK Đại số 10): Nêu định nghĩa của tanα , cotα và giải thích vì sao ta có :
tan(α + kπ) = tanα, k ∈Z;
cot(α + kπ) = cotα, k ∈Z;
Lời giải

+) Nếu k lẻ: k = 1+2m ; m ∈ Z , ta có:



Bài 3 (trang 155 SGK Đại số 10): Tính:

Lời giải



Kiến thức áp dụng

Bài 4 (trang 155 SGK Đại số 10): Rút gọn biểu thức :

Lời giải






Bài 5 (trang 156 SGK Đại số 10): Tính :

Lời giải

Bài 6 (trang 156 SGK Đại số 10): Không sử dụng máy tính, hãy chứng minh:

Lời giải




Bài 7 (trang 156 SGK Đại số 10): Chứng minh các đồng nhất thức sau đây:

Lời giải



Bài 8 (trang 156 SGK Đại số 10): Chứng minh các biểu thức sau không phụ thuộc x

Lời giải




Soanbaitap.com gửi đến các bạn học sinh đầy đủ những bài giải toán 10 có trong sách giáo khoa tập 1 và tập 2, đầy đủ cả phần hình học và đại số. Tổng hợp các công thức, giải bài tập toán và cách giải toán lớp 10 khác nhau.
#soanbaitap
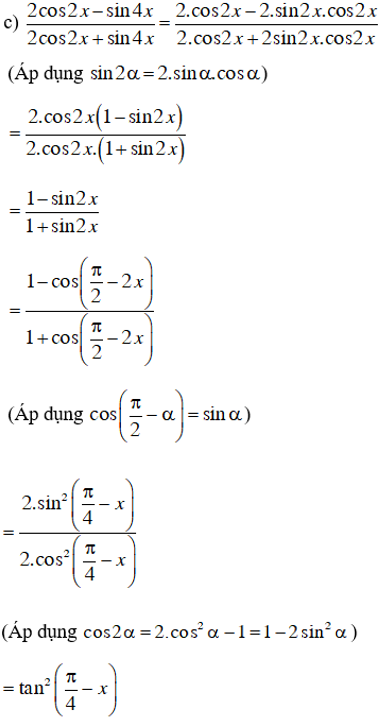
Không có nhận xét nào:
Đăng nhận xét