Bài 1 (trang 91 SGK Hình học 12): Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1)
a) Chứng minh A, B, C, D là bốn đỉnh của một tứ diện.
b) Tìm góc giữa hai đường thẳng AB và CD
c) Tính độ dại đường cao của hình chóp A.BCD
Lời giải:

a) Cách 1:
Phương trình đoạn chắn (ABC) là:
 hay x + y + z – 1 = 0.
hay x + y + z – 1 = 0.
Thay tọa độ điểm D(-2; 1; -1) ta được: (-2) + 1 + (-1) – 1 = -3 ≠ 0
⇒ D không nằm trong (ABC)
⇒ A, B, C, D không đồng phẳng
⇒ A, B, C, D là bốn đỉnh của một tứ diện.
Cách 2:

⇒ A, B, C, D không đồng phẳng
⇒ A, B, C, D là bốn đỉnh của hình tứ diện.

c) Độ dài đường cao hình chóp A.BCD chính là khoảng cách từ A đến (BCD).

⇒ (BCD) nhận  là 1 vtpt
là 1 vtpt
⇒ (BCD): x – 2y – 2z + 2 = 0
⇒ Độ dài đường cao hình chóp A.BCD là:

Bài 3 (trang 92 SGK Hình học 12): Cho bốn điểm A(-2; 6; 3), B(1; 0; 6), C(0; 2; -1), D(1; 4; 0)
a) Viết phương trình mặt phẳng (BCD). Suy ra ABCD là một tứ diện.
b) Tính chiều cao AH của tứ diện ABCD.
c) Viết phương trình mặt phẳng (α) chứa AB và song song với CD.
Lời giải:
a) 
(BCD) nhận  là 1 vtpt
là 1 vtpt
⇒ (BCD): 16x – 6y – 4z + 8 = 0
hay (BCD): 8x – 3y – 2z + 4 = 0.
b) Chiều cao AH của tứ diện ABCD chính là khoảng cách từ điểm A đến mp (BCD) :


(α) chứa AB và song song với CD
⇒ (α) nhận (1; 0; -1) là 1 vtpt
(α) đi qua A(-2; 6; 3)
⇒ (α): x – z + 5 = 0.
Kiến thức áp dụng
+ A, B, C, D là bốn đỉnh của một tứ diện nếu chúng không đồng phẳng.
+ Khoảng cách từ điểm M(x0 ; y0 ; z0) đến mặt phẳng (P) : ax + by + cz + d = 0 là :

Bài 4 (trang 92 SGK Hình học 12): Lập phương trình tham số của đường thẳng:
a) Đi qua hai điểm A(1 ; 0 ; -3) và B(3 ; -1 ; 0).
b) Đi qua M(2 ; 3 ; -5) và song song với đường thẳng (Δ): 
Lời giải:
a) Đường thẳng AB nhận  là 1 vtcp và đi qua A(1; 0; -3)
là 1 vtcp và đi qua A(1; 0; -3)
 b) (Δ) nhận
b) (Δ) nhận  là 1 vtcp
là 1 vtcp
+ (d) cần tìm song song với (Δ)
⇒ (d) nhận  là 1 vtcp
là 1 vtcp
+ (d) đi qua M(2; 3; -5)
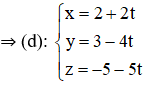
+ Phương trình tham số của đường thẳng đi qua điểm M(x0 ; y0 ; z0) và nhận vec tơ  là 1 vtcp là :
là 1 vtcp là :
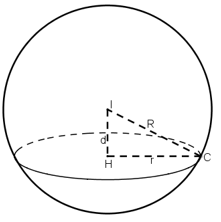
Bài 5 (trang 92 SGK Hình học 12): Cho mặt cầu(S) có phương trình (x – 3)2 + (y + 2)2 + (z – 1)2 = 100 và mặt phẳng (α) có phương trình 2x – 2y – z + 9 = 0. Mp(α) cắt mặt cầu (S) theo một đường tròn (C). Hãy xác định tọa độ tâm và tính bán kính của đường tròn (C).
Lời giải:
 Kiến thức áp dụng
Kiến thức áp dụng
+ Phương trình mặt cầu tâm I(a ; b ; c), bán kính R là :
(S) : (x – a)2 + (y – b)2 + (z – c)2 = R2.
+ Mặt phẳng (α) cắt mặt cầu (S) tâm I, bán kính R có thiết diện là một đường tròn bán kính r, ta luôn có:

#soanbaitap
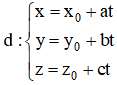
Không có nhận xét nào:
Đăng nhận xét