Ôn tập chương 1 - soanbaitap.com

Bài 1 (trang 40 SGK Đại số 11):

a.Hàm số y = cos3x có phải là hàm số chẵn không?Tại sao?

b.Hàm số y = tan(x+ π/5) có phải là hàm số lẻ không?Tại sao?

Lời giải:

a. y = f(x) = cos3x là hàm số chẵn vì:

+ TXĐ: D = R ⇒ ∀ x ∈ D ta có: - x ∈ D

+ f(-x) = cos3.(-x) = cos(-3x) = cos 3x = f(x) ∀ x ∈ D

b. Ta có:

⇒ g(x) không phải hàm số lẻ.

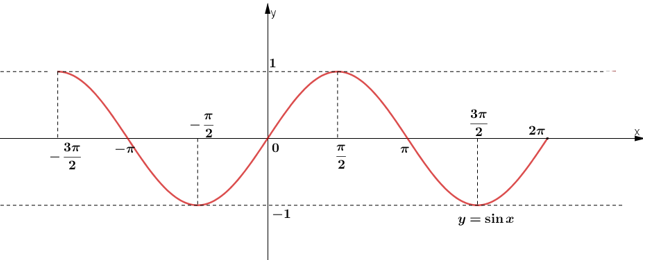
Bài 2 (trang 40 SGK Đại số 11): Căn cứ vào đồ thị hàm số y = sinx, tìm những giá trị của x trên đoạn[-3π/2 ; 2π] để hàm số đó:

a. Nhận giá trị bằng – 1

b. Nhận giá trị âm

Lời giải:

Xét đồ thị hàm số y = sin x trên  :

a. sin x = -1 ⇔ 

(Hoành độ giao điểm của đồ thị hàm số và đường thẳng y = -1).

b. sin x < 0

⇔ x ∈ (-π; 0) ∪ (π; 2π)

(Các khoảng mà đồ thị nằm phía dưới trục hoành).

Bài 3 (trang 41 SGK Đại số 11): Tìm giá trị lớn nhất của các hàm số sau:

Lời giải:

Ta có: với mọi x ∈ R : -1 ≤ cos x ≤ 1

⇒ 0 ≤ 1 + cos x ≤ 2

⇒ 0 ≤ 2(1 + cos x) ≤ 4

y = 3 ⇔ cos x = 1 ⇔ x = k.2π (k ∈ Z).

Vậy giá trị lớn nhất của hàm số đạt được là 3 khi x = k.2π (k ∈ Z).

Vậy giá trị lớn nhất của hàm số đạt được là 1 khi  (k ∈ Z).

Kiến thức áp dụng

+ Với mọi x ∈ R ta luôn có: -1 ≤ sin x ≤ 1; -1 ≤ cos x ≤ 1.

Bài 4 (trang 41 SGK Đại số 11): Giải phương trình sau:

Lời giải:

Vậy phương trình có tập nghiệm

{arcsin – 1 + k2π; π - arcsin – 1 + k2π} (k ∈ Z)

 

Vậy phương trình có họ nghiệm  (k ∈ Z)

* Lưu ý: Về cách gộp, tách, loại họ nghiệm xem lại phần kiến thức áp dụng bài 5 trang 29. Không nhất thiết phải gộp các họ nghiệm lại.

c. Điều kiện:  (k ∈ Z).

Vậy phương trình có tập nghiệm 

 

d. Điều kiện:

Vậy phương trình có tập nghiệm 

Kiến thức áp dụng

+ Phương trình sin x = sin α có nghiệm 

+ Phương trình cos x = cos α có nghiệm x = ±α + k.2π (k ∈ Z).

+ Phương trình tan x = tan α có nghiệm x = α + k.π, (k ∈ Z)

+ Phương trình cot x = cot α có nghiệm x = α + k.π, (k ∈ Z).

+ Với các phương trình chứa tan và cot phải có điều kiện xác định.

Bài 4 (trang 41 SGK Đại số 11): Giải phương trình sau:

Lời giải:

Vậy phương trình có tập nghiệm

{arcsin – 1 + k2π; π - arcsin – 1 + k2π} (k ∈ Z)

 

Vậy phương trình có họ nghiệm  (k ∈ Z)

* Lưu ý: Về cách gộp, tách, loại họ nghiệm xem lại phần kiến thức áp dụng bài 5 trang 29. Không nhất thiết phải gộp các họ nghiệm lại.

c. Điều kiện:  (k ∈ Z).

Vậy phương trình có tập nghiệm 

 

d. Điều kiện:

Vậy phương trình có tập nghiệm 

Kiến thức áp dụng

+ Phương trình sin x = sin α có nghiệm 

+ Phương trình cos x = cos α có nghiệm x = ±α + k.2π (k ∈ Z).

+ Phương trình tan x = tan α có nghiệm x = α + k.π, (k ∈ Z)

+ Phương trình cot x = cot α có nghiệm x = α + k.π, (k ∈ Z).

+ Với các phương trình chứa tan và cot phải có điều kiện xác định.

Bài 6 (trang 41 SGK Đại số 11): Phương trình cos x = sin x có số nghiệm thuộc đoạn [-π; π] là:

A. 2

B. 4

C. 5

D. 6

Lời giải:

Chọn đáp án A.

Giải thích:

sin x = cos x

⇒ tan x = 1

Vậy phương trình có hai nghiệm thuộc [-π; π]

Bài 7 (trang 41 SGK Đại số 11): Phương trình ...

Lời giải:

Chọn đáp án A.

Giải thích:

(1) ⇔ cos4x = sin 2x

⇔ 1 – 2sin²2x = sin2x

Suy ra, phương trình đã cho có 2 nghiệm thuộc khoảng 

Kiến thức áp dụng

cos2a = 2cos²a – 1 = 1 – 2sin²a = cos²a – sin²a.

Bài 8 (trang 41 SGK Đại số 11): Nghiệm dương nhỏ nhất của phương trình sin x + sin 2x = cos x + 2 cos²x là:

Lời giải:

Chọn đáp án C.

Giải thích :

Cách 1: sin x + sin2x = cosx + 2cos²x

⇔ sin x + 2sinx.cosx = cosx(1 + 2cosx)

⇔ sinx (1 + 2cosx) = cosx.(1 + 2cosx)

⇔ (sin x – cos x)(1 + 2.cos x) = 0

Cách 2: Thử các đáp án nhận thấy chỉ có  và  là nghiệm của phương trình.

 nên chọn 

Bài 9 (trang 41 SGK Đại số 11): Nghiệm âm lớn nhất của phương trình 2tan²x + 5 tanx + 3 = 0 là:

Lời giải:

Chọn đáp án B.

Giải thích :

Ta có: 2tan²x + 5 tan x + 3 = 0

Soanbaitap.com gửi đến các bạn học sinh đầy đủ những bài giải toán 11 có trong sách giáo khoa tập 1 và tập 2, đầy đủ cả phần hình học và đại số. Tổng hợp các công thức, giải bài tập toán và cách giải toán lớp 11 khác nhau.

 

 

 

 

#soanbaitap