Bài 2 (trang 79 SGK Đại Số 10): Cho số x > 5, số nào trong các số sau đây là số nhỏ nhất?
Lời giải
Với mọi x ≠ 0 ta luôn có: - 1 < 0 < 1. Do đó,
hay C < A < B.
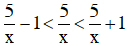
Lại có x > 5 ⇒ x2 > 52 (Bình phương hai vế)
⇒ 
(Nhân cả hai vế của bất đẳng thức với 
)
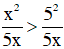
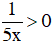
Vậy ta có C < A < B và C < A < D nên trong bốn số trên, C là số nhỏ nhất.
Kiến thức áp dụng
+ Cộng cả hai vế của BĐT với một số bất kì, bất đẳng thức không đổi chiều
a < b ⇔ a + c < b + c
+ Nâng hai vế của bất đẳng thức lên một lũy thừa bậc chẵn:
0 < a < b ⇔ a2n < b2n với mọi n ∈ N*.
+ Nhân cả hai vế của BĐT với một số dương thì BĐT không đổi chiều:
a < b ⇔ a.c < b.c với mọi c > 0.
Bài 2 (trang 79 SGK Đại Số 10): Cho số x > 5, số nào trong các số sau đây là số nhỏ nhất?
Lời giải
Với mọi x ≠ 0 ta luôn có: - 1 < 0 < 1. Do đó,
hay C < A < B.
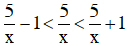
Lại có x > 5 ⇒ x2 > 52 (Bình phương hai vế)
⇒ (Nhân cả hai vế của bất đẳng thức với )
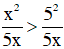
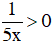
Vậy ta có C < A < B và C < A < D nên trong bốn số trên, C là số nhỏ nhất.
Kiến thức áp dụng
+ Cộng cả hai vế của BĐT với một số bất kì, bất đẳng thức không đổi chiều
a < b ⇔ a + c < b + c
+ Nâng hai vế của bất đẳng thức lên một lũy thừa bậc chẵn:
0 < a < b ⇔ a2n < b2n với mọi n ∈ N*.
+ Nhân cả hai vế của BĐT với một số dương thì BĐT không đổi chiều:
a < b ⇔ a.c < b.c với mọi c > 0.
Bài 3 (trang 79 SGK Đại Số 10): Cho a, b, c là độ dài ba cạnh của một tam giác.
a) Chứng minh (b - c)2 < a2
b) Từ đó suy ra: a2 + b2 + c2 < 2(ab + bc + ca)
Lời giải
a) Vì a, b, c là độ dài 3 cạnh của một tam giác
⇒ a + c > b và a + b > c (Bất đẳng thức tam giác)
⇒ a + c – b > 0 và a + b – c > 0
Ta có: (b – c)2 < a2
⇔ a2 – (b – c)2 > 0
⇔ (a – (b – c))(a + (b – c)) > 0
⇔ (a – b + c).(a + b – c) > 0 (Luôn đúng vì a + c – b > 0 và a + b – c > 0).
Vậy ta có (b – c)2 < a2 (1) (đpcm)
b) Chứng minh tương tự phần a) ta có :
( a – b)2 < c2 (2)
(c – a)2 < b2 (3)
Cộng ba bất đẳng thức (1), (2), (3) ta có:
(b – c)2 + (c – a)2 + (a – b)2 < a2 + b2 + c2
⇒ b2 – 2bc + c2 + c2 – 2ca + a2 + a2 – 2ab + b2 < a2 + b2 + c2
⇒ 2(a2 + b2 + c2) – 2(ab + bc + ca) < a2 + b2 + c2
⇒ a2 + b2 + c2 < 2(ab + bc + ca) (đpcm).
Bài 5 (trang 79 SGK Đại Số 10): Chứng minh rằng:
Lời giải
Đặt t = √x (điều kiện t ≥ 0), khi đó
= t8 – t5 + t2 – t + 1
Ta cần chứng minh : t8 – t5 + t2 – t + 1 > 0
Cách 1 (theo hướng dẫn ở đề bài).
+ Xét 0 ≤ t < 1 ⇒ t3 < 1 ⇒ 1 – t3 > 0 ; 1 – t > 0
t8 – t5 + t2 – t + 1 = t8 + (t2 – t5) + (1 – t)
= t8 + t2.(1 – t3) + (1 – t)
> 0 + 0 + 0 = 0
( vì t8 ≥ 0; t2 ≥ 0 ⇒ t2(1 - t3) ≥ 0 )
+ Xét t ≥ 1 ⇒ t3 ≥ 1 ⇒ t3 – 1 ≥ 0 và t – 1 ≥ 0.
t8 – t5 + t2 – t + 1 = t5.(t3 – 1) + t.(t – 1) + 1
≥ 0 + 0 + 1 > 0
Vậy với mọi t ≥ 0 thì t8 – t5 + t2 – t + 1 ≥ 1/2 > 0 hay 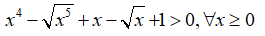(đpcm)
Cách 2:
2.(t8 – t5 + t2 – t + 1) = t8 + t8 – 2t5 + t2 + t2 – 2t + 1 + 1
= t8 + (t4 – t)2 + (t – 1)2 + 1.
≥ 0 + 0 + 0 + 1 = 1.
(Vì t8 ≥ 0 ; (t4 – t)2 ≥ 0; (t – 1)2 ≥ 0)
⇒ t8 – t5 + t2 – t + 1 ≥ 1/2 > 0 hay 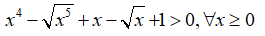(đpcm)
Bài 6 (trang 79 SGK Đại Số 10): Trong mặt phẳng tọa độ Oxy, trên các tia Ox và Oy lần lượt lấy các điểm A và B thay đổi sao cho đường thẳng AB luôn tiếp xúc với đường tròn tâm O bán kính 1. Xác định tọa độ của A và B để đoạn AB có độ dài nhỏ nhất.
Lời giải
Gọi tiếp điểm của AB và đường tròn tâm O, bán kính 1 là M, ta có: OM ⊥ AB.
ΔOAB vuông tại O, có OM là đường cao nên MA.MB = MO2 = 1 (hằng số)
Áp dụng bất đẳng thức Cô-si ta có:
MA + MB ≥ 2√MA.MB = 2. √1 = 2
Dấu « = » xảy ra khi MA = MB = 1.
Khi đó OA = √(MA2 + MO2) = √2 ; OB = √(OM2 + MB2) = √2.
Mà A, B nằm trên tia Ox và Oy nên A(√2; 0); B(0; √2)
Vậy tọa độ là A(√2, 0) và B(0, √2).
Soanbaitap.com gửi đến các bạn học sinh đầy đủ những bài giải toán 10 có trong sách giáo khoa tập 1 và tập 2, đầy đủ cả phần hình học và đại số. Tổng hợp các công thức, giải bài tập toán và cách giải toán lớp 10 khác nhau.
#soanbaitap
màn hình hiện ra x2 = –0.637458608
thì phương trình (1) trở thành 3x – 2 = 2x + 3. Từ đó x = 5.
thì phương trình (1) trở thành 2 – 3x = 2x + 3. Từ đó 
là một nghiệm của phương trình (3).
và x = –1.
, khi đó |2x + 5| = 2x + 5
, khi đó |2x + 5| = –2x – 5.
(1)
(2)
(3)
(4)
với mọi x.