Ôn tập chương I – Căn bậc hai. Căn bậc ba - soanbaitap.com

Lý thuyết

1. Ta có x = √a

2. Điều kiện tồn tại của √A là A ≥ 0.

3.

4. với A ≥ 0; B ≥ 0

Tổng quát với A₁ ≥ 0 (1 ≤ i ≤ n).

5. Với A ≥ 0; B > 0 ta có .

6. Khi đưa thừa số A² ra ngoài dấu căn bậc hai ta được |A|.

; B ≥ 0

7. Đưa thừa số vào trong dấu căn bậc hai

8. Khử mẫu của biểu thức dưới dấu căn bậc hai.

Đối với biểu thức dưới dấu căn, ta nhân mẫu số với thừa số phụ thích hợp để mẫu số có dạng C²

9. Trục căn thức ở mẫu số

Gồm các dạng cơ bản sau:

(Lưu ý: Nhân cả tử và mẫu với một thừa số thích hợp để mẫu có dạng: )

10. Một số chú ý giải phương trình

Câu 1: Tìm giá trị của x để biểu thức sau có nghĩa

Hướng dẫn:

Câu 2: Tính giá trị của biểu thức

Hướng dẫn:

Câu 3: Rút gọn các biểu thức sau:

Hướng dẫn:

c) Ta có

Câu 4: Giải các phương trình sau đây

Hướng dẫn:

a) Điều kiện: x ≥ 1/2.

b) Điều kiện: x ≥ -2

Ta có

1. Mức độ Nhận biết – Thông hiểu

Câu 1: Với giá trị nào của x thì mỗi biểu thức sau có nghĩa ?

Câu 2: Tính giá trị của các biểu thức sau:

Câu 3: Rút gọn các biểu thức sau :

Câu 4: So sánh các số sau:

Câu 5: Giải các phương trình sau:

2. Mức độ Vận dụng – Vận dụng cao.

Câu 1: Cho biểu thức

với x > 0, x ≠ 0.

a) Rút gọn biểu thức V.

b) Tìm giá trị của x để V = 1/3.

Câu 2: Giải các phương trình sau:

Câu 3: Cho biểu thức:

, với x ≥ 0, x ≠ 1.

a) Rút gọn biểu thức P.

b) Cho biểu thức, với x ≥ 0, x ≠ 1, x ≠ 4. Chứng minh Q ≥ 6

Câu 4: Cho hai biểu thức

với x ≥ 0, x ≠ 25.

a. Tính giá trị biểu thức A khi x = 9.

b. Chứng minh rằng

c. Tìm tất cả các giá trị của x để A = B.|x - 4|.

Câu 5: Tìm x, y, z biết rằng

Câu 6: Chứng minh rằng:

a) Với mọi n ∈ Z⁺, ta có:

b) Với mọi n ∈ Z⁺, ta có:

Câu 7: Rút gọn các biểu thức sau:

Câu 8: Tính

a) Tính GTLN của biểu thức

, biết x + y = 4.

b) Tính GTNN của biểu thức

với 0 < x < 1

Câu 9: Cho biểu thức

(với x ≥ 0; x ≠ 1).

a) Chứng minh

b) Chứng minh rằng nếu x ≥ 0; x ≠ 1 thì P ≤ 3/2.

Câu 10: Cho biểu thức

(với x > 0; x ≠ 1).

a) Rút gọn biểu thức A.

b) Có bao nhiêu giá trị nguyên của x để

Câu 11:

a) Cho x, y là hai số thực thỏa mãn Chứng minh rằng:

b) Cho các số thực x, y thỏa mãn

Tính giá trị của biểu thức:

c) Tính giá trị của biểu thức:

1 (trang 39 SGK Toán 9 Tập 1). Nêu điều kiện để x là căn bậc hai số học của số a không âm. Cho ví dụ

Trả lời:

Để x là căn bậc hai số học của số a không âm là x ≥ a và x² = a.

Ví dụ 2 là căn bậc hai số học của 4 vì 2 > 0 và 2² = 4.

2 (trang 39 SGK Toán 9 Tập 1): Chứng minh √a² = |a| với mọi số a.

Trả lời:

3 (trang 39 SGK Toán 9 Tập 1): Biểu thức A phải thỏa mãn điều kiện gì để √A xác định prôtêin

Trả lời:

√A xác định khi A > 0 hay nói cách khác : điều kiện xác định của căn bậc hai là biểu thức lấy căn không âm.

4 (trang 39 SGK Toán 9 Tập 1): Phát biểu và chứng minh định lí về mối liên hệ giữa phép nhân và phép khai phương. Cho ví dụ.

Trả lời:

5 (trang 39 SGK Toán 9 Tập 1): Phát biểu và chứng minh định lí về mối liên hệ giữa phép chia và phép khai phương. Cho ví dụ.

Trả lời:

Bài 71 (trang 40 SGK Toán 9 Tập 1): Rút gọn các biểu thức sau:

 

Lời giải:

= (2√2 - 3√2 + 10)√2 - √5

= 2.(√2)² - 3.(√2)² + √10.√2 - √5

= 4 - 6 + √20 - √5 = -2 + 2√5 - √5

= -2 + √5

= 0,2.10.√3 + 2|√3 - √5|

s

= 2√3 + 2(√5 - √3)

= 2√3 + 2√5 - 2√3 = 2√5

Bài 72 (trang 40 SGK Toán 9 Tập 1): Phân tích thành nhân tử (với các số x, y, a, b không âm và a ≥ b)

Lời giải:

a) xy - y√x + √x - 1

= (√x)².y - y√x + √x - 1

= y√x(√x - 1) + √x - 1

= (√x - 1)(y√x + 1) với x ≥ 1

= √x(√a + √b) - √y(√a + √b)

= (√a + √b)(√x - √y) (với x, y, a và b đều không âm)

(với a + b, a - b đều không âm)

d) 12 - √x - x

= 16 - x - 4 - √x (tách 12 = 16 - 4 và đổi vị trí)

= [4² - (√x)²] - (4 + √x)

= (4 - √x)(4 + √x) - (4 + √x)

= (4 + √x)(4 - √x - 1)

= (4 + √x)(3 - √x)

Bài 74 (trang 40 SGK Toán 9 Tập 1): Tìm x, biết:

 

Lời giải:

⇔ -2x + 1 = 3

⇔ -2x = 2

⇔ x = -1 (thỏa mãn)

Vậy phương trình có 2 nghiệm: x = 2 và x = -1

Bài 75 (trang 40 SGK Toán 9 Tập 1): Chứng minh các đẳng thức sau:

Lời giải:

Biến đổi vế trái:

= (-√7 - √5)(√7 - √5)

= -(√7 + √5)(√7 - √5)

= -(7 - 5) = -2 = VP (đpcm)

= (1 + √a)(1 - √a)

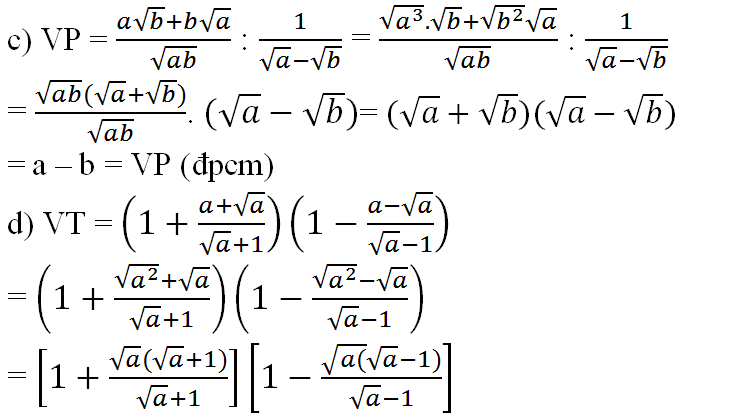
= 1 - (√a)² = 1 - a = VP (đpcm)

 

Soanbaitap.com gửi đến các bạn học sinh đầy đủ những bài giải toán 9 có trong sách giáo khoa tập 1 và tập 2, đầy đủ cả phần Toán hình 9 và Toán đại 9. Tổng hợp các công thức, giải bài tập toán và cách giải toán lớp 9 khác nhau.

 

 

 

 

 

 

 

 

 

 

 

#soanbaitap