1. Phương pháp
Ta trình bày phép chia tương tự như cách chia các số tự nhiên. Với hai đa thức A và B của một biến, B≠0 tồn tại duy nhất hai đa thức Q và R sao cho:
A = B.Q + R, với R=0 hoặc bậc của R nhỏ hơn bậc của B.
Nếu R=0, ta được phép chia hết.
Nếu R≠0, ta được phép chia có dư.
Ví dụ: Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia:
a, ( x3 - 7x + 3 - x2 ):( x - 3 ).
b, ( 5x3 + 7 - 3x2 ):( x2 + 1 ).
Hướng dẫn:
a) Ta có:

Khi đó ta có: ( x3 - 7x + 3 - x2 ) = ( x - 3 ).( x2 + 2x - 1 )
b) Ta có

Khi đó ta có ( 5x3 + 7 - 3x2 ) = ( x2 + 1 )( 5x - 3 ) - 5x + 10.
Bài 1: Thực hiện các phép chia
a, ( 2x3 - 26x - 24 ):( x2 + 4x + 3 )
b, ( x3 - 9x2 + 28x - 30 ):( x - 3 )
Hướng dẫn:
a) Ta có phép chia

Vậy ( 2x3 - 26x - 24 ) = ( x2 + 4x + 3 )( 2x - 8 )
b) Ta có phép chia

Vậy ( x3 - 9x2 + 28x - 30 ) = ( x - 3 )( x2 - 6x + 10 )
Bài 2: Tính nhanh các phép chia sau:
a, ( x6 + 2x3y2 + y4 ):( x3 + y2 )
b, ( 625x4 - 1 ):[ ( 5x + 1 )( 5x - 1 ) ]
Hướng dẫn:
a) Ta có ( x6 + 2x3y2 + y4 ):( x3 + y2 ) = ( x3 + y2 )2:( x3 + y2 ) = ( x3 + y2 )
Vậy ( x6 + 2x3y2 + y4 ):( x3 + y2 ) = ( x3 + y2 )
b) Ta có ( 625x4 - 1 ):[ ( 5x + 1 )( 5x - 1 ) ] = [ ( 25x2 - 1 )( 25x2 + 1 ) ]:( 25x2 - 1 ) = ( 25x2 + 1 )
Vậy ( 625x4 - 1 ):[ ( 5x + 1 )( 5x - 1 ) ] = ( 25x2 + 1 )
Bài 3: Tìm các số nguyên n để giá trị của biểu thức n3 + 6n2 -7n + 4 chia hết cho giá trị của biểu thức n - 2.
Hướng dẫn:
Ở đây, ta có thực hiện đặt phép chia như câu 1 để tìm số dư và tìm điều kiện giá trị của n để thỏa mãn đề bài. Nhưng bài này ta làm cách biến đổi như sau:
Ta có n3 + 6n2 -7n + 4 = ( n3 - 3n2.2 + 3.n.22 - 8 ) + 12n2 - 19n + 12
= ( n - 2 )3 + 12n( n - 2 ) + 5( n - 2 ) + 22
Khi đó ta có: (n3 + 6n2 - 7n + 4)/(n - 2) = ( n - 2 )2 + 12n + 5 + 22/(n - 2)
Để giá trị của biểu thức n3 + 6n2 -7n + 4 chia hết cho giá trị của biểu thức n - 2.
⇔ ( n - 2 ) ∈ UCLN( 22 ) = {± 1; ± 2; ± 11; ± 22 }
⇒ n ∈ {- 20; - 9; 0; 1; 3; 4; 13; 24 }
Vậy các giá trị nguyên của n cần tìm là n ∈ { - 20; - 9; 0; 1; 3; 4; 13; 24 }
Trả lời câu hỏi Toán 8 Tập 1 Bài 12 trang 30: Kiểm tra lại tích (x2 – 4x – 3)(2x2 – 5x + 1) có bằng (2x4 - 13x3 + 15x2 + 11x – 3) hay không.
Lời giải
Vậy (x2 – 4x – 3)(2x2 – 5x + 1) = 2x4 - 13x3 + 15x2 + 11x – 3
Bài 67 (trang 31 SGK Toán 8 Tập 1): Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia:
a) (x3 – 7x + 3 – x2) : (x – 3);
b) (2x4 – 3x3 – 3x2 – 2 + 6x) : (x2 – 2)
Lời giải:
a) x3 – 7x + 3 – x2 = x3 – x2 – 7x + 3
Thực hiện phép chia:

Vậy (x3 – x2 – 7x + 3) : (x – 3) = x2 + 2x – 1
b) 2x4 – 3x3 – 3x2 – 2 + 6x = 2x4 – 3x3 – 3x2 + 6x – 2
Thực hiện phép chia:
Vậy (2x4 – 3x3 – 3x2 + 6x – 2) : (x2 – 2) = 2x2 – 3x + 1.
Bài 68 (trang 31 SGK Toán 8 Tập 1): Áp dụng hằng đẳng thức đáng nhớ để thực hiện phép chia:
a) (x2 + 2xy + y2) : (x + y)
b) (125x3 + 1) : (5x + 1)
c) (x2 – 2xy + y2) : (y – x)
Lời giải:
a) (x2 + 2xy + y2) : (x + y)
= (x + y)2 : (x + y)
= x + y
b) (125x3 + 1) : (5x + 1)
= [(5x)3 + 1] : (5x + 1)
= (5x + 1)[(5x)2 – 5x + 1]] : (5x + 1)
= (5x)2 – 5x + 1
= 25x2 – 5x + 1
c) (x2 – 2xy + y2) : (y – x)
= (x – y)2 : [-(x – y)]
= -(x – y)
= y – x
Hoặc (x2 – 2xy + y2) : (y – x)
= (y2 – 2yx + x2) : (y – x)
= (y – x)2 : (y – x)
= y – x
Bài 69 (trang 31 SGK Toán 8 Tập 1): Cho hai đa thức: A = 3x4 + x3 + 6x – 5 và B = x2 + 1. Tìm dư R trong phép chia A cho B rồi viết A dưới dạng A = B.Q + R
Lời giải:
Thực hiện phép chia ta có:
Vậy 3x4 + x3 + 6x – 5 = (x2 + 1).(3x2 + x – 3) + 5x – 2.
Bài 70 (trang 32 SGK Toán 8 Tập 1): Làm tính chia:
a) (25x5 – 5x4 + 10x2) : 5x2 ;
b) (15x3y2- 6x2y – 3x2y2) : 6x2y
Lời giải:
a) (25x5 – 5x4 + 10x2) : 5x2
= 25x5 : 5x2 + (-5x4) : 5x2 + 10x2 : 5x2
= (25 : 5).(x5 : x2) + (-5 : 5).(x4 : x2) + (10 : 5).(x2 : x2)
= 5.x5 – 2 + (-1).x4 – 2 + 2.1
= 5x3 – x2 + 2
b) (15x3y2 – 6x2y – 3x2y2) : 6x2y
= (15x3y2 : 6x2y) + (-6x2y) : 6x2y + (-3x2y2) : 6x2y
= (15 : 6).(x3 : x2).(y2 : y) + (-6 : 6).(x2 : x2).(y : y) + (-3 : 6).(x2 : x2).(y2 : y)

Kiến thức áp dụng
– Để chia đa thức A cho đơn thức B, ta chia từng hạng tử của đa thức A cho đơn thức B rồi cộng các kết quả với nhau.
– Muốn chia đơn thức A cho đơn thức B ta làm như sau :
+ Chia hệ số của đơn thức A cho hệ số của đơn thức B
+ Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
+ Nhân các kết quả vừa tìm được với nhau.
Bài 71 (trang 32 SGK Toán 8 Tập 1): Không thực hiện phép chia, hãy xét xem đa thức A có chia hết cho đa thức B hay không.

Lời giải:
Do đó A = 15x4 - 8x3 + x2 chia hết cho  hay A chia hết cho B.
hay A chia hết cho B.
b) A = x2 - 2x + 1 = (x – 1)2
Vậy A chia hết cho x – 1 hay A chia hết cho B.
Kiến thức áp dụng
Đa thức A (đã được rút gọn) chia hết cho đơn thức B nếu mỗi hạng tử của đa thức A đều chia hết cho đơn thức B.
Đơn thức A chia hết cho đơn thức B khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.
Bài 71 (trang 32 SGK Toán 8 Tập 1): Không thực hiện phép chia, hãy xét xem đa thức A có chia hết cho đa thức B hay không.

Lời giải:
Do đó A = 15x4 - 8x3 + x2 chia hết cho  hay A chia hết cho B.
hay A chia hết cho B.
b) A = x2 - 2x + 1 = (x – 1)2
Vậy A chia hết cho x – 1 hay A chia hết cho B.
Kiến thức áp dụng
Đa thức A (đã được rút gọn) chia hết cho đơn thức B nếu mỗi hạng tử của đa thức A đều chia hết cho đơn thức B.
Đơn thức A chia hết cho đơn thức B khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.
Bài 73 (trang 32 SGK Toán 8 Tập 1): Tính nhanh:
a) (4x2 – 9y2) : (2x – 3y) ;
b) (27x3 – 1) : (3x – 1)
c) (8x3 + 1) : (4x2 – 2x + 1) ;
d) (x2 – 3x + xy – 3y) : (x + y)
Lời giải:
a) (4x2 – 9y2) : (2x – 3y)
(Sử dụng HĐT để phân tích số bị chia thành tích)
= [(2x)2 – (3y)2] : (2x – 3y)
(Xuất hiện hằng đẳng thức (3))
= (2x – 3y)(2x + 3y) : (2x – 3y)
= 2x + 3y.
b) (27x3 – 1) : (3x – 1)
(Sử dụng HĐT để phân tích số bị chia thành tích)
= [(3x)3 – 1] : (3x – 1)
(Xuất hiện hằng đẳng thức (7))
= (3x – 1).[(3x)2 + 3x.1 + 12] : (3x – 1)
= (3x – 1).(9x2 + 3x + 1) : (3x – 1)
= 9x2 + 3x + 1
c) (8x3 + 1) : (4x2 – 2x + 1)
(Sử dụng HĐT để phân tích số bị chia thành tích)
= [(2x)3 + 1] : (4x2 – 2x + 1)
(Xuất hiện HĐT (6))
= (2x + 1).[(2x)2 - 2x.1 + 12] : (4x2 – 2x + 1)
= (2x + 1).(4x2 - 2x + 1) : (4x2 – 2x + 1)
= 2x + 1.
d) (x2 – 3x + xy – 3y) : (x + y)
(Nhóm hạng tử để phân tích số bị chia thành tích)
= [(x2 – 3x) + (xy – 3y)] : (x + y)
= [x.(x – 3) + y.(x – 3)] : (x + y)
= (x + y).(x – 3) : (x + y)
= x – 3.
Kiến thức áp dụng
Hằng đẳng thức cần nhớ :
A2 – B2 = (A – B).(A + B) (2)
A3 + B3 = (A + B)(A2 – AB + B2) (6)
A3 – B3 = (A – B)(A2 + AB + B2) (7)
Bài 74 (trang 32 SGK Toán 8 Tập 1): Tìm số a để đa thức 2x3 – 3x2 + x + a chia hết cho đa thức x + 2.
Lời giải:
Cách 1: Thực hiện phép chia:
2x3 – 3x2 + x + a chia hết cho x + 2
⇔ số dư = a – 30 = 0
⇔ a = 30.
Cách 2: Phân tích 2x3 – 3x2 + x + a thành nhân tử có chứa x + 2.
2x3 – 3x2 + x + a
= 2x3 + 4x2 – 7x2 – 14x + 15x + 30 + a – 30
(Tách -3x2 = 4x2 – 7x2; x = -14x + 15x)
= 2x2(x + 2) – 7x(x + 2) + 15(x + 2) + a – 30
= (2x2 – 7x + 15)(x + 2) + a – 30
2x3 – 3x2 + x + a chia hết cho x + 2 ⇔ a – 30 = 0 ⇔ a = 30.
Soanbaitap.com gửi đến các bạn học sinh đầy đủ những bài giải toán 8 có trong sách giáo khoa tập 1 và tập 2, đầy đủ cả phần Toán Đại 8 và Toán Hình 8. Tổng hợp các công thức, giải bài tập toán và cách giải toán lớp 8 khác nhau
#soanbaitap
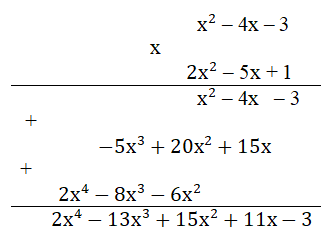
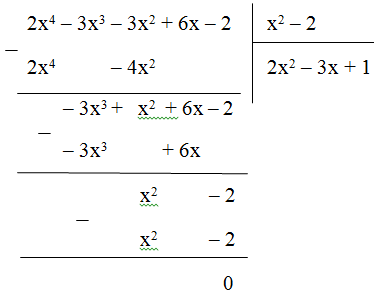
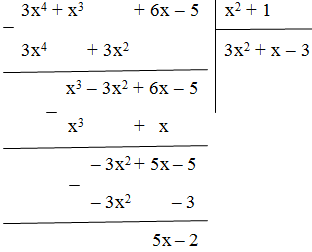
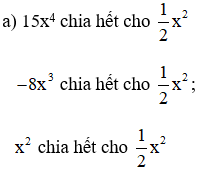

Không có nhận xét nào:
Đăng nhận xét