a) Đưa một thừa số ra ngoài dấu căn
Với hai biểu thức A, B mà B ≥ 0 ta có

Ví dụ:

b) Đưa thừa số vào trong dấu căn
Với A ≥ 0, B ≥ 0 thì 
Với A < 0, B ≥ 0 thì 
Ví dụ:

c) Khử mẫu của biểu thức dưới dấu căn.
Với AB ≥ 0 và B ≠ 0 thì

Ví dụ:

d) Trục căn thức ở mẫu
Trục căn thức ở mẫu số là biến đổi để biểu thức đó mất căn thức ở mẫu số
• Với các biểu thức A, B mà B > 0 ta có: 
Ví dụ:

• Với các biểu thức A, B, C mà A ≥ 0, A ≠ B2, ta có:

Ví dụ:

• Với các biểu thức A, B, C mà A ≥ 0, B ≥ 0, A ≠ B ta có:

Ví dụ:

- Để rút gọn biểu thức chứa căn bậc hai, ta cần vận dụng phối hợp các phép tính và các phép biến đổi đã biết.
- Khi rút gọn một dãy các phép tính cộng, trừ, nhân, chia, lũy thứa và khai phương thì thứ tự thực hiện: khai căn trước rồi đến lũy thừa, sau đó đến nhân, chia, cộng, trừ
Câu 1: Cho biểu thức
 (với x ≥ 0; x ≠ 1 và x ≠ 1/4).
(với x ≥ 0; x ≠ 1 và x ≠ 1/4).
Tìm tất cả các giá trị của x để B < 0.
Câu 2: Giải các phương trình sau:

Câu 3: Rút gọn các biểu thức sau:

Câu 4: Chứng minh rằng
 (n ∈ N; n ≥ 2)
(n ∈ N; n ≥ 2)
Trả lời câu hỏi Toán 9 Tập 1 Bài 6 trang 24: Với a ≥ 0, b ≥ 0, chứng tỏ √(a2 b) = a√b.
Lời giải
√(a2 b) = √(a2 ).√b = |a| √b = a√b (do a ≥ 0;b ≥ 0)
Bài 43 (trang 27 SGK Toán 9 Tập 1): Viết các số hoặc biểu thức dưới dấu căn thành dạng tích rồi đưa thừa số ra ngoài dấu căn.

Lời giải:

Bài 44 (trang 27 SGK Toán 9 Tập 1): Đưa thừa số vào trong dấu căn.

Lời giải:
(Chú ý: Muốn đưa thừa số vào trong căn thì thừa số phải là số không âm. Chẳng hạn như ở phần b, c thì chúng ta không đưa dấu "-" vào trong căn.)

Bài 44 (trang 27 SGK Toán 9 Tập 1): Đưa thừa số vào trong dấu căn.

Lời giải:
(Chú ý: Muốn đưa thừa số vào trong căn thì thừa số phải là số không âm. Chẳng hạn như ở phần b, c thì chúng ta không đưa dấu "-" vào trong căn.)

Bài 46 (trang 27 SGK Toán 9 Tập 1): Rút gọn các biểu thức sau với x ≥ 0:

Lời giải:
a) Với x ≥ 0 thì √3x có nghĩa. Ta có:

b) Với x ≥ 0 thì √2x có nghĩa. Ta có:
Bài 47 (trang 27 SGK Toán 9 Tập 1): Rút gọn:

Lời giải:

(có |x + y| = x + y do x + y > 0 vì x ≥ 0, y ≥ 0 và x ≠ y)

(có |a| = a do a > 0,5 và |1 - 2a| = 2a - 1 vì 2a - 1 > 0 do a > 0,5)
Soanbaitap.com gửi đến các bạn học sinh đầy đủ những bài giải toán 9 có trong sách giáo khoa tập 1 và tập 2, đầy đủ cả phần Toán hình 9 và Toán đại 9. Tổng hợp các công thức, giải bài tập toán và cách giải toán lớp 9 khác nhau.
#soanbaitap
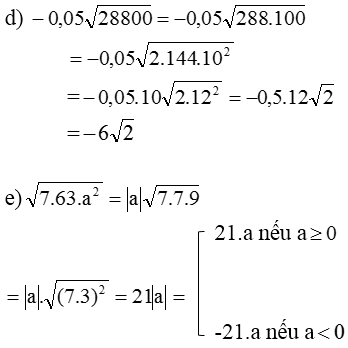
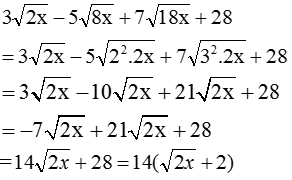
Không có nhận xét nào:
Đăng nhận xét