A. Lý thuyết
Câu 1: Phát biểu định nghĩa hai góc đối đỉnh.
Lời giải chi tiết:
Định nghĩa: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Câu 2: Phát biểu định lí về hai góc đối đỉnh.
Lời giải chi tiết:
Định lý: Hai góc đối đỉnh thì bằng nhau.
Câu 3: Phát biểu định nghĩa hai đường thẳng vuông góc.
Lời giải chi tiết:
Định nghĩa: Hai đường thẳng (xx’, yy’ ) cắt nhau và trong các góc tạo thành có một góc vuông được gọi là hai đường thẳng vuông góc. Kí hiệu là (xx’ ⊥ yy’)
Câu 4: Phát biểu định nghĩa đường trung trực của một đoạn thẳng.
Lời giải chi tiết:
Định nghĩa: Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng ấy.
Câu 5: Phát biểu dấu hiệu (định lí) nhận biết hai đường thẳng song song.
Lời giải chi tiết:
Nếu đường thẳng (c) cắt hai đường thẳng (a, b) và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì (a) và (b) song song với nhau.
Câu 6: Phát biểu tiên đề Ơ – clit về đường thẳng song song.
Lời giải chi tiết:
Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Câu 7: Phát biểu tính chất (định lí) của hai đường thẳng song song.
Lời giải chi tiết:
Nếu một đường thẳng cắt hai đường thẳng song song thì:
a) Hai góc so le trong bằng nhau;
b) Hai góc đồng vị bằng nhau;
c) Hai góc trong cùng phía bù nhau.
Câu 8: Phát biểu định lí về hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba.
Lời giải chi tiết:
Định lý: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Câu 9: Phát biểu định lí về hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba.
Lời giải chi tiết:
Định lý: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
Câu 10: Phát biểu định lí về một đường thẳng vuông góc với một trong hai đường thẳng song song.
Lời giải chi tiết:
Định lý: Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
B. Bài tập
Giải bài 54 trang 103 SGK Toán 7 tập 1.
Đề bài: Trong hình 37 có 5 cặp đường thẳng vuông góc với bốn cặp đường thẳng song song. Hãy quan sát rồi viết tên các cặp đường thẳng đó và kiểm tra lại bằng êke .
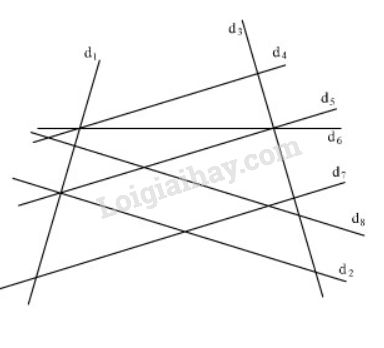
- Phương pháp giải - Xem chi tiết
Quan sát hình vẽ để dự đoán các cặp đường thẳng song song, sau đó kiểm tra lại bằng êke.
- Lời giải chi tiết
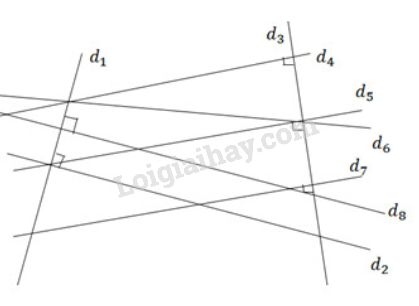
Năm cặp đường thẳng vuông góc là:
d1⊥d8;d1⊥d2;
d3⊥d4;d3⊥d5;
d3⊥d7
Bốn cặp đường thẳng song song là:
d4//d5;d4//d7;
Giải bài 55 trang 103 SGK Toán 7 tập 1.
Đề bài: Vẽ lại hình 38 rồi vẽ thêm:
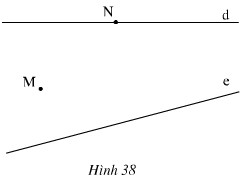
a) Các đường thẳng vuông góc với d đi qua M, đi qua N.
b) Các đường thẳng song song với e đi qua M, đi qua N.
- Phương pháp giải - Xem chi tiết
Dùng thước kẻ và êke để vẽ các đường thẳng vuông góc và các đường thẳng song song.
- Lời giải chi tiết
a) Các đường thẳng vuông góc với d đi qua M, đi qua N:

b) Các đường thẳng song song với e đi qua M, đi qua N:

Giải bài 56 trang 104 SGK Toán 7 tập 1.
Đề bài: Cho đoạn thẳng AB dài 28mm. Hãy vẽ đường trung trực của đoạn thẳng ấy.
- Phương pháp giải - Xem chi tiết
Đường trung trực của AB phải vuông góc với AB và đi qua trung điểm I của AB.
- Lời giải chi tiết
Cách vẽ:
- Dùng thước có chia khoảng vẽ đoạn thẳng AB=28mm.
- Vẽ trung điểm I của đoạn AB bằng cách lấy I∈AB sao cho AI=14mm.
- Dùng ê kê vẽ đường thẳng d vuông góc với AB tại I.
Đường thẳng d chính là đường trung trực của AB.

Giải bài 56 trang 104 SGK Toán 7 tập 1.
Đề bài: Cho đoạn thẳng AB dài 28mm. Hãy vẽ đường trung trực của đoạn thẳng ấy.
- Phương pháp giải - Xem chi tiết
Đường trung trực của AB phải vuông góc với AB và đi qua trung điểm I của AB.
- Lời giải chi tiết
Cách vẽ:
- Dùng thước có chia khoảng vẽ đoạn thẳng AB=28mm.
- Vẽ trung điểm I của đoạn AB bằng cách lấy I∈AB sao cho AI=14mm.
- Dùng ê kê vẽ đường thẳng d vuông góc với AB tại I.
Đường thẳng d chính là đường trung trực của AB.

Giải bài 58 trang 104 SGK Toán 7 tập 1.
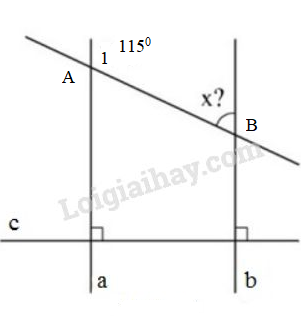
Đề bài: Tính số đo x trong hình 40. Hãy giải thích vì sao tính được như vậy?

- Phương pháp giải - Xem chi tiết
- Áp dụng định lí: "hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau" để chứng minh hai đường thẳng song song.
- Áp dụng tính chất: nếu một đường thẳng cắt hai đường thẳng song song thì hai góc trong cùng phía bù nhau.
- Lời giải chi tiết
Gọi tên như hình vẽ.

Ta có: a⊥c,b⊥c
Theo định lí : hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau. Do đó a//b
⇒A1^+B^=1800 (hai góc ở vị trí trong cùng phía bù nhau)
⇒115o+x=180o
⇒x=180o–115o=65o
Vậy
Giải bài 59 trang 104 SGK Toán 7 tập 1.
Đề bài: Hình 41 cho biết d//d′//d″ và hai góc 600,1100. Tính các góc E1^,G2^,G3^,D4^,A5^,B6^.

- Phương pháp giải - Xem chi tiết
- Áp dụng tính chất: nếu một đường thẳng cắt hai đường thẳng song song thì:
a) Hai góc so le trong bằng nhau;
b) Hai góc đồng vị bằng nhau;
c) Hai góc trong cùng phía bù nhau.
- Hai góc đối đỉnh thì bằng nhau.
- Tổng số đo hai góc kề bù bằng 180o.
- Lời giải chi tiết

+) Vì d′//d″ có: E1^ và C^=60o là hai góc so le trong nên E1^=60o
+) Vì d′//d″ có: G2^ và BDd′^=110o là hai góc đồng vị nên G2^=110o
+) G2^+G^3=180o (hai góc kề bù)
⇒G3^=180o−G2^=180o−110o=70o
+) D4^=BDd′^=110o (vì hai góc đối đỉnh)
+) Vì d//d″ nên A5^=E1^=60o (vì hai góc đồng vị)
+) Vì d//d″ nên B6^=G3^=700 (vì hai góc đồng vị)
Vậy E1^=60o,G2^=110o,G3^=70o,
Giải bài 60 trang 104 SGK Toán 7 tập 1.
Đề bài: Hãy phát biểu các định lí được diễn tả bằng các hình vẽ sau rồi viết giả thiết, kết luận của từng định lí (xem Bài 5).
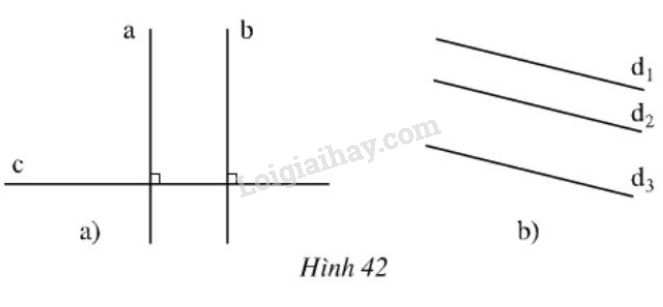
- Phương pháp giải - Xem chi tiết
Một tính chất được khẳng định là đúng bằng suy luận được gọi là định lí.
Định lí thường phát biểu dưới dạng: " Nếu A thì B" với A là giả thiết, là điều kiện cho biết; B là kết luận, là điều được suy ra.
- Lời giải chi tiết
a) Định lí: Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.

Hoặc: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó sẽ vuông góc với đường thẳng còn lại.
b) Định lí: Nếu hai đường thẳng cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.

Soanbaitap.com gửi đến các bạn học sinh đầy đủ những bài giải toán 7 có trong sách giáo khoa tập 1 và tập 2, đầy đủ cả phần Toán Đại 7 và Toán Hình 7. Tổng hợp các công thức, giải bài tập toán và cách giải toán lớp 7 khác nhau
#soanbaitap
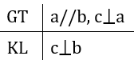
Không có nhận xét nào:
Đăng nhận xét